Quadruple-precision floating-point format

In computing, quadruple precision (also commonly shortened to quad precision) is a binary floating-point computer number format that occupies 16 bytes (128 bits) in computer memory.

In IEEE 754-2008 the 128-bit base-2 format is officially referred to as binary128.

Floating-point precisions

IEEE 754:
16-bit: Half (binary16)
32-bit: Single (binary32), decimal32
64-bit: Double (binary64), decimal64
128-bit: Quadruple (binary128), decimal128
Other:
Minifloat · Extended precision
Arbitrary precision

Contents

IEEE 754 quadruple-precision binary floating-point format: binary128

The IEEE 754 standard specifies a binary128 as having:

The format is written with an implicit lead bit with value 1 unless the exponent is stored with all zeros. Thus only 112 bits of the significand appear in the memory format, but the total precision is 113 bits (approximately 34 decimal digits, 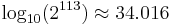\log_{10}(2^{113}) \approx 34.016). The bits are laid out as follows:

Exponent encoding

The quadruple-precision binary floating-point exponent is encoded using an offset binary representation, with the zero offset being 16383; also known as exponent bias in the IEEE 754 standard.

Thus, as defined by the offset binary representation, in order to get the true exponent the offset of 16383 has to be subtracted from the stored exponent.

The stored exponents 0x0000 and 0x7fff are interpreted specially.

Exponent Significand zero Significand non-zero Equation
0x0000 0, −0 subnormal numbers 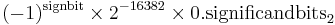(-1)^{\text{signbit}} \times 2^{-16382} \times 0.\text{significandbits}_2
0x0001, ..., 0x7ffe normalized value 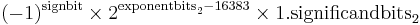(-1)^{\text{signbit}} \times 2^{{\text{exponentbits}_2} - 16383} \times 1.\text{significandbits}_2
0x7fff ±infinity NaN (quiet, signalling)

The maximum representable value is ≈ 1.1897 × 104932.

Quadruple-precision examples

These examples are given in bit representation, in hexadecimal, of the floating-point value. This includes the sign, (biased) exponent, and significand.

3fff 0000 0000 0000 0000 0000 0000 0000   = 1
c000 0000 0000 0000 0000 0000 0000 0000   = -2

7ffe ffff ffff ffff ffff ffff ffff ffff   ≈  1.189731495357231765085759326628007 × 104932 (max quadruple precision)

0000 0000 0000 0000 0000 0000 0000 0000   = 0
8000 0000 0000 0000 0000 0000 0000 0000   = -0

7fff 0000 0000 0000 0000 0000 0000 0000   = infinity
ffff 0000 0000 0000 0000 0000 0000 0000   = -infinity

3ffd 5555 5555 5555 5555 5555 5555 5555   ≈  1/3

By default, 1/3 rounds down like double precision, because of the odd number of bits in the significand. So the bits beyond the rounding point are 0101... which is less than 1/2 of a unit in the last place.

Double-double arithmetic

A common software technique to implement nearly quadruple precision using pairs of double-precision values is sometimes called double-double arithmetic.[1][2][3] Using pairs of IEEE double-precision values with 53-bit significands, double-double arithmetic can represent operations with at least[1] a 2×53=106-bit significand (and possibly 107 bits via clever use of the sign bit[4]), only slightly less precise than the 113-bit significand of IEEE binary128 quadruple precision. The range of a double-double remains essentially the same as the double-precision format because the exponent has still 11 bits,[1] significantly lower than the 15-bit exponent of IEEE quadruple precision (a range of 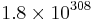1.8\times10^{308} for double-double versus 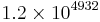1.2\times10^{4932} for binary128).

In particular, a double-double/quadruple-precision value q in the double-double technique is represented implicitly as a sum q=x+y of two double-precision values x and y, each of which supplies half of q's significand.[2] That is, the pair (x,y) is stored in place of q, and operations on q values (+,−,×,...) are transformed into equivalent (but more complicated) operations on the x and y values. Thus, arithmetic in this technique reduces to a sequence of double-precision operations; since double-precision arithmetic is commonly implemented in hardware, double-double arithmetic is typically substantially faster than more general arbitrary-precision arithmetic techniques.[2][1]

Implementations

Quadruple precision is almost always implemented in software by a variety of techniques (such as the double-double technique above, although that technique does not implement IEEE quadruple precision), since direct hardware support for quadruple precision is extremely rare. One can use general arbitrary-precision arithmetic libraries to obtain quadruple (or higher) precision, but specialized quadruple-precision implementations may achieve higher performance.

Computer-language support

A separate question is the extent to which quadruple-precision types are directly incorporated into computer programming languages.

Quadruple precision is specified in Fortran by the REAL*16 or REAL(KIND=16) type, although this type is not supported by all compilers. (Quadruple-precision REAL*16 is supported by the Intel Fortran Compiler[5] and by the GNU Fortran compiler[6] on x86, x86-64, and Itanium architectures, for example.)

In the C/C++ with a few systems and compilers, quadruple precision may be specified by the long double type, but this is not required by the language (which only requires long double to be at least as precise as double), nor is it common. On x86 and x86-64, the most common C/C++ compilers implement long double as either 80-bit extended precision (e.g. the GNU C Compiler gcc[7] and the Intel C++ compiler with a /Qlong‑double switch[8]) or simply as being synonymous with double precision (e.g. Microsoft Visual C++[9]), rather than as quadruple precision. On a few other architectures, some C/C++ compilers implement long double as quadruple precision, e.g. gcc on PowerPC (as double-double[10][11][12]) and SPARC,[13] or the Sun Studio compilers on SPARC.[14] Even if long double is not quadruple precision, however, some C/C++ compilers provide a nonstandard quadruple-precision type as an extension. For example, gcc provides a quadruple-precision type called __float128 for x86, x86-64 and Itanium CPUs,[15] and some versions of Intel's C/C++ compiler for x86 and x86-64 supply a nonstandard quadruple-precision type called _Quad.[16]

Hardware support

Native support of 128-bit floats is defined in SPARC V8[17] and V9[18] architectures (e.g. there are 16 quad-precision registers %q0, %q4, ...), but no SPARC CPU implements quad-precision operations in hardware.[19]

As at 2005, there are no native 128-bits FPUs.[20]

Non-IEEE extended-precision (128 bit of storage, 1 sign bit, 7 exponent bit, 112 fraction bit, 8 bits unused) was added to the System/370 series and was available on some S/360 models (S/360-85[21], -195, and others by special request or simulated by OS software).

See also

References

  1. ^ a b c d Yozo Hida, X. Li, and D. H. Bailey, Quad-Double Arithmetic: Algorithms, Implementation, and Application, Lawrence Berkeley National Laboratory Technical Report LBNL-46996 (2000). Also Y. Hida et al., Library for double-double and quad-double arithmetic (2007).
  2. ^ a b c J. R. Shewchuk, Adaptive Precision Floating-Point Arithmetic and Fast Robust Geometric Predicates, Discrete & Computational Geometry 18:305-363, 1997.
  3. ^ Knuth, D. E.. The Art of Computer Programming (2nd ed.). chapter 4.2.3. problem 9.. 
  4. ^ Robert MunafoF107 and F161 High-Precision Floating-Point Data Types (2011).
  5. ^ "Intel Fortran Compiler Product Brief". Su. http://h21007.www2.hp.com/portal/download/files/unprot/intel/product_brief_Fortran_Linux.pdf. Retrieved 2010-01-23. 
  6. ^ "GCC 4.6 Release Series - Changes, New Features, and Fixes". http://gcc.gnu.org/gcc-4.6/changes.html. Retrieved 2010-02-06. 
  7. ^ i386 and x86-64 Options, Using the GNU Compiler Collection.
  8. ^ Intel Developer Site
  9. ^ MSDN homepage, about Visual C++ compiler
  10. ^ RS/6000 and PowerPC Options, Using the GNU Compiler Collection.
  11. ^ Inside Macintosh - PowerPC Numerics
  12. ^ 128-bit long double support routines for Darwin
  13. ^ SPARC Options, Using the GNU Compiler Collection.
  14. ^ The Math Libraries, Sun Studio 11 Numerical Computation Guide (2005).
  15. ^ Additional Floating Types, Using the GNU Compiler Collection
  16. ^ Intel C++ Forums (2007).
  17. ^ The SPARC Architecture Manual: Version 8. SPARC International, Inc. 1992. http://www.sparc.com/standards/V8.pdf. Retrieved 2011-09-24. "SPARC is an instruction set architecture (ISA) with 32-bit integer and 32-, 64-, and 128-bit IEEE Standard 754 floating-point as its principal data types." 
  18. ^ David L. Weaver, Tom Germond, ed (1994). The SPARC Architecture Manual: Version 9. SPARC International, Inc. http://www.sparc.org/standards/SPARCV9.pdf. Retrieved 2011-09-24. "Floating-point: The architecture provides an IEEE 754-compatible floating-point instruction set, operating on a separate register file that provides 32 single-precision (32-bit), 32 double-precision (64-bit), 16 quad-precision (128-bit) registers, or a mixture thereof." 
  19. ^ "SPARC Behavior and Implementation". Numerical Computation Guide — Sun Studio 10. Sun Microsystems, Inc. 2004. http://download.oracle.com/docs/cd/E19059-01/stud.10/819-0499/ncg_sparc.html. Retrieved 2011-09-24. "There are four situations, however, when the hardware will not successfully complete a floating-point instruction: ... The instruction is not implemented by the hardware (such as ... quad-precision instructions on any SPARC FPU)." 
  20. ^ J. Fujimoto, T. Ishikawa, D. Perret-Gallix (2005-05-05). High precision numerical computations — A case for an HAPPY design. http://fcppl.in2p3.fr/cgi-bin/twiki.source/pub/ACAT/PresentationsNotes/Highprecisionnumericalcomputatio3.pdf. Retrieved 2011-09-24. "But today there are no straight 128-bit floating point unit providing quadruple precision available." 
  21. ^ "Structural aspects of the system/360 model 85: III extensions to floating-point architecture", Padegs, A., IBM Systems Journal, Vol:7 No:1 (March 1968), pp. 22–29

External links